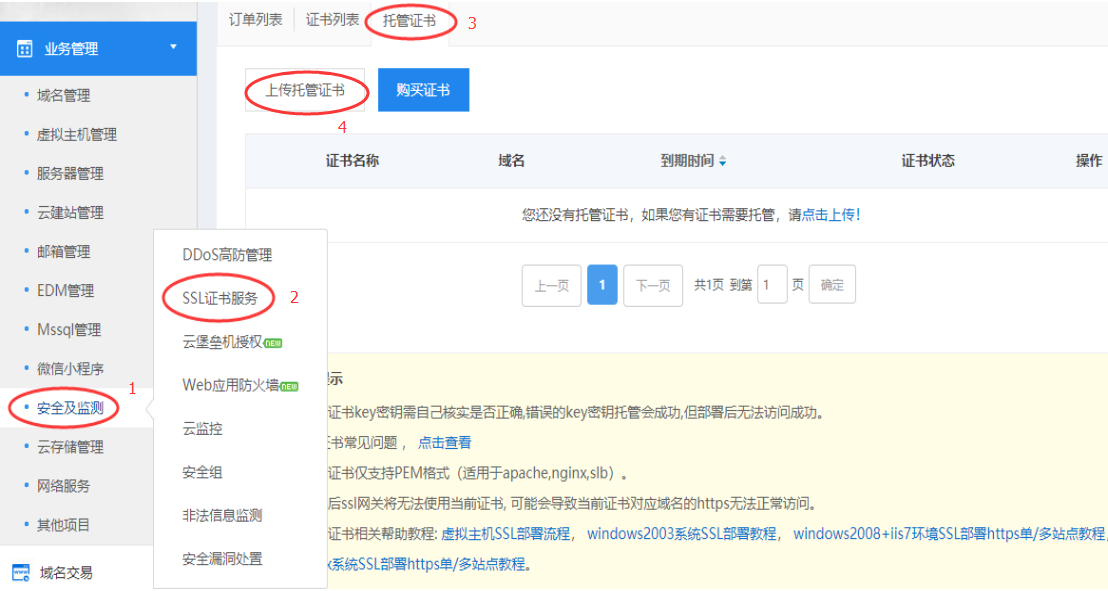
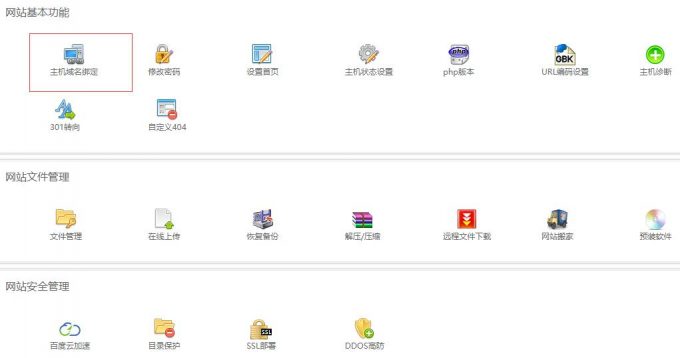
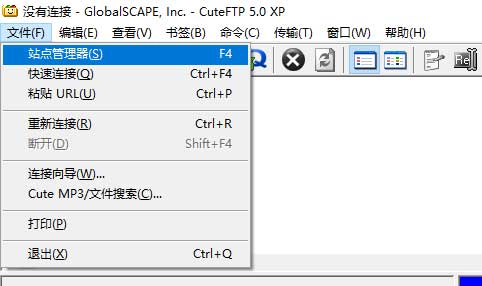
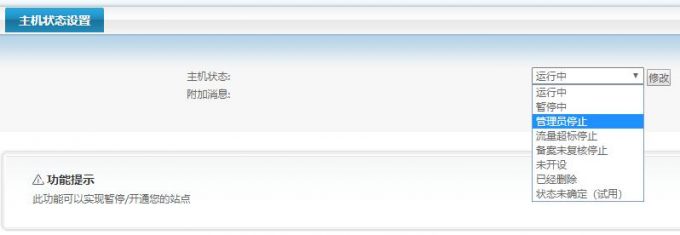
总磷曲线斜率怎么算(吸光度计算例题)
对于微积分来说,其中的微分学最基本的思想便是在曲线上求出定点P的切线的斜率。
不精确的切线定义
在过去,人们曾凭借生活经验对切线做出了定义,感觉两个物体在表面有接触,便有了相切的感觉。
在几何中对于一个圆,一条直线只和它有一个交点,便是交点的切线;要是相穿过这个圆,就有两个不同的交点,就不能算是切线了。如下图:

于是人们就对切线下了定义了,说一条直线只和对应曲线只相交于一点就是切线。这个定义确实能适应一些相切的情况,但是下面的就不能解释了:

图中a直线明明没有相切的感觉,却只有一个交点;b直线与曲线相交于多个点,却在A点有和曲线相切的直观印象。很明显这个切线的定义还不完善。
精确的切线定义
数学是个严谨的科学,上面这种不清晰的定义让那些思维严谨的数学家实在受不了。终于在1630年左右法国有一个数学家叫费尔马,他忍无可忍蹦了出来给出了一个让自己舒畅无比的切线定义,这个定义如此重要,以至于对我们今天的数学、物理学以及其它学科的发展起到了不可或缺的作用。
曲线切线的精确定义:假设有一个曲线y=f(x),它上面有一个点P,在P的右边(左边也可以)有一个点Q,做一条直线PQ穿过这两点,这时候这直线PQ就和曲线y相交于两个点,你可能会想,这不还是两个点吗?这下连相切的感觉都没了。不着急那个费马尔思维的闪光点是后面这句:如果点Q沿着曲线y逐渐向P滑动,那么这根直线也会不断的改变张角,一直到这个Q无限的接近P时,相切的感觉就有了,此时P几乎和Q重合,直线PQ和曲线y相切于P点了。

精彩的不光是定义,还有背后的极限思想。现在这个定义妥妥的解决了上面那两幅图的情况。
切线斜率的计算方法
这时候问题又来了,切线我知道是怎么回事了,不是说有个叫“导数”的东西其实就是曲线上一个点的切线的斜率吗?就拿上面说的P点,那么随意一个,我该怎么算斜率呢?


我们还是找了一个P点坐标为(x0,y0),在y上又找了一个Q(x1,y1)点,按照费尔马的想法,我们做直线PQ,很明显直线PQ切割了曲线y,有两个交点,这个时候我们可以计算出这个切割状态下的直线PQ的斜率:

k'代表直线PQ在切割状态下的斜率
当我们让Q沿着y曲线的轨迹滑向P点时,这个Q点的坐标值是不断的变化的,直线PQ一直通过P点,但是它对于x轴的倾斜程度在不断的变化,并不断的接近P点的切线这个极限方向,因此我们想这个切线的斜率k,就是Q趋近于P时不断变化的k'的极限值:

Q点向P点趋近过程中x1的值不断的趋近x0,y1也是一样的情形
这个式子看起来个头越来越大了,不过不要担心,这只不过是用数学符号lim表示了这种沿曲线滑动最终无限趋近一个点的动态情景。
到这里我们想计算的这个切线斜率k好像可以着手计算了,但是那里面都是字母怎么算呢?我们可以先想一下,既然这个式子表示的是动态过程,我们就从动态的方法去想。lim是无限趋近的意思,那么Q无限趋近P时y1无限趋近于y0,那么y1-y0趋近于0;同理x1-x0也趋近于0:

完了,不管你会不会做,反正除以0的我是没办法。还记的上高等数学时老师怎么说的吗?把y用x表示:

这样把那个分子分母上下相同部分消掉,就求出来了。做是这么做,但是为什么呀?凡是总得有个理由吧,这个理由就是我们用x表示y之后,因为x1趋近于x0这个动作引发的分子无限变小的因素x1-x0就从分子里给分离出来了,注意是无限变小的因素。还有一点重要的就是无限趋近和相等是不一样的,不论怎么接近,x1与x0总是差那么一点点,那这时候就有疑问了,大上面的式子里不是明明写着0/0吗?我们要说的是只有在lim的加持下表示出了这个趋近动作时,才说:

但实际上不论怎么靠近:

所以要注意极限和相等的不同含义。这样的话我们就能求出切线的斜率了,因为在无限趋近的情况下x1的极限就是x0(注意我没说x1是x0):

好啦,随便一个在y上点的切线斜率居然是这个点的横坐标的2倍,真是不可思议,崇拜费尔马的力量吧。